utm 51 區的標準割線與在台灣附近的誤差
gis 第二次作業,要以 utm 投影與台灣作題材,主題自訂。 然後內容必須包括 utm 簡介與在台灣地區的誤差。 我簡單計算了 utm 51 區的標準尺度割線位置, 並取了台灣島上幾個點計算與比較 utm、twd97、大地線的誤差。
utm 介紹
utm 是主要由美國軍方使用的地圖投影, 使用範圍是全世界除南北極區外的地區。 utm 使用橫麥卡托投影法, 將全地球每 6° 經度分為一 區, 共分為 60 帶,數字編號。 並緯度每 8° 分為一 帶, 分為 23 帶,以英文字母編號。 但帶與區並非絕對,在地球上數處有例外。
起源
最早使用 utm 這個名稱的是二戰德國時的德意志國防軍, 用來做航空照片的投影。 當時的一些航空照片上註記了 UTMREF 與分區、分帶的編碼, 並以橫麥卡托投影展示,但中央經線尺度為 1.0 ^1 。 在二戰後 1947 年,美國陸軍採用了非常類似的系統, 亦稱為 utm,但將中央經線尺度改為 0.9996。
橫麥托投影原理
橫麥卡托投影是將假想的圓柱與地軸垂直, 並圓柱與地球上一經線相切(或相割), 並與麥卡托相同是由地心射出光源, 可保相切部份,也就是地球上南北狹長帶狀地區的變形為最小。 但在遠離中央經線地區尺度會放大, 有如麥卡托投影在南北極區的放大。 故橫卡托投影適用於南北狹長型的國家,
橫麥卡托投影法與麥卡托的相似點, 在於同樣使用圓柱與地球相切,並由球心作為光源投影。 在投影出的成果上,其實與麥卡托投影相差甚多。 因為投影方向垂直,如果要以單一經圈投影出整個地球, 在相差 90° 的經圈上會最大的扭曲, 且扭曲後的世界地圖,也與麥卡托投影的扭大不相同。
但麥卡托與橫麥卡托在扭曲不大的小範圍內仍會顯得相似, 因為球面與圓柱相切處附近, 橫麥卡托投影的經緯線是約略垂直的, 相較之下麥卡托投影則在全球範圍都是垂直的。
相切或相割
橫麥卡托投影可以是與球面相切或相割: (許多投影法都可以。) 如果是相切,就是在中央經線上不變型, 但其它區域,離中央經線越遠,就放越大。 如果是相割,則會在二條割線上是不變型, 割線間則會縮小,割線外會放大。 相割相對相切,會有較多區域處在尺度 1±x 的範圍內, 而相切則全在都 1+2x 的範圍。
台灣本島現今採用的是相割投影, 因考慮台灣島雖然是南北狹長型, 但中央經線通過地區,多是中央山脈山區, 聚落與開發地區則分布在東西部。 若採用相切,則不變型的地區都在山區, 東西部反而變型較大,也就是重要的地區變型較大, 不變型的地區卻不重要, 違反我們希望地圖投影能在關注地區的扭曲為最小的目標。
而相割則可以有二條標準尺度的割線, 分別貫穿東西部平原, 也就是在台灣島東西二側的變型尺度會較小, 符合我們地圖投影的目標。 而現今的 utm 投影,則為了整體的變型要較小, 所以也採用了相割的投影法, 讓投影造成的誤差控制在 1.0 附近。
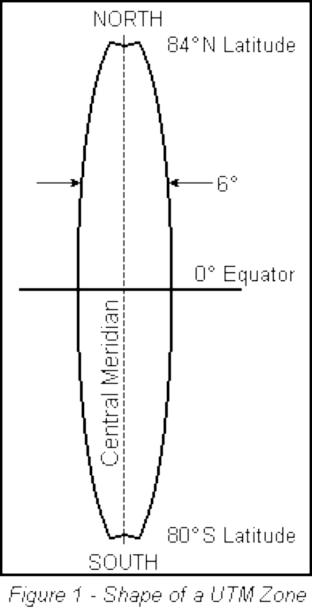
utm 分區形狀
utm 為橫麥卡托,雖然在標準經線上能不變型, 但由於地球是球形,在高緯度地區經線會收束; 如果 utm 仍全整投影出同樣寛度的區域, 在不同分區的 utm 在高緯度地區會重覆。
utm 的作法是在高緯度地區減少每區的寬度, 從二區重疊部份的中線分隔, 所以 utm 每區成為了楔形,又因為 utm 不包含極區, 楔型的尖端被去除,成為以下的形狀:
平常我們所見的 utm 則多半是畫成一張完整的圖, 其類似於將楔形拉伸成長方型的結果, 只是方便想像地球作為整體的成果:
實際上若將 utm 完整展示, 應該是一條條的楔形並列, 在赤道以外的區域都不會相連。
utm 網格座標
utm 與許多平面座標系統相同,為了避免出現負數座標值,會將原點西移。 原點的東西方向座標從原本的中央經線,西移 500 公里。 而原點的南北方向座標則是從赤道起算,若位在南半球, 則將原點南移 10000 公里。
台灣與 utm
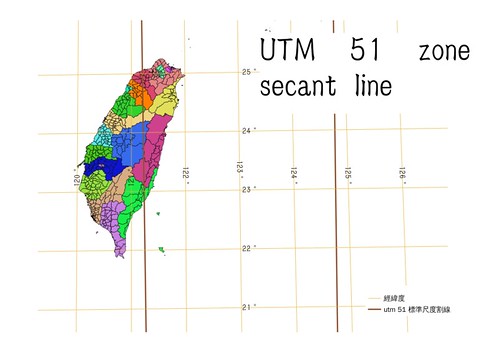
在早期國民政府遷台時,由於地圖為軍事機密不公開, 曾採用全球製圖的 utm 作為地型圖的座標系統 ^2 。 utm 為 6° 分帶,含蓋台灣地區的圖幅為 51 zone, 也就是橫跨 120-126°E 的範圍。
當年所使用的 utm51 區座標系統, 相比台灣現今的 twd97 二度分帶系統, 原點都在赤道上, 但 twd97 的東西方向原點則是在 121°E 上西移 250 公里。
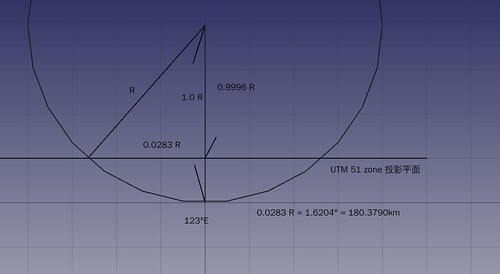
而 utm 的標準尺度線位置,可以由計算得到。 若 utm 的中央經線尺度為 0.9996, 依據投影原理,距離與尺度成正比, 也就是 utm 的投影平面與地表在中央經線處 離地心的距離比為 0.9996 : 1, 如下圖所示:
因此可以推出 UTM 51 區的標準尺度線約在中央經線左右 180km 處,
換算成經度的話,由於處在北緯 23° ,
需要將球面上的 1.6204° 乘上當地緯度造成的變化:
1.6204° ÷ cos(23°) = 1.7603° ,
也就是 utm 51 區在台灣緯度 23°N 附近的標準尺度線
約在 123±1.7603°E,接近台灣的一條則在 121.2397°E。
其實相當接近台灣島中線。
twd97 與 twd67
open source geographic wiki 上提到幾種方法區別 twd67 與 twd97 地圖, 其中一種是看東北角的三貂角燈塔座標 ^3 : 若是東經 122 度線穿過三貂角東方外海,則是 twd67; 若是東經 122 度線穿過三貂角西部陸地,則是 twd97。
- 東北角三貂角燈塔東邊外海就是東經 122 度整. 若是 TWD97 時, 則 122 度線穿越過燈塔西側.
- 國道一號新竹公道五交流道為東經 121 度 Expressway 1's Gongdaowu interchange lies upon 121.00 deg. E. == 250000m E.
- 台北市復興南路為 Taibei City's Fuxing S. Rd. lies upon 304000m E.
- 豐原火車站前為 221000m E. lies in front of Fengyuan railway station.
根據 tgos 圖台查詢,現今所三貂角燈塔的 twd97 平面座標為
(351085.6949, 2766970.4467) ,
使用 proj.4 轉換回 twd97 的橢球 invproj +init=epsg:3826 +ellps=GRS80 ,
結果是 (122d0'5.293"E 25d0'26.632"N) ,
燈塔的確在 122°E 東邊。
utm 在台灣的投影誤差
utm 是將地球每六度經度分為一帶, 在每帶使用橫麥卡托投影, 以中央經線尺度為 0.9996 的相割投影。 在台灣是 utm 51 zone,120°E 到 126°E 的地區。
由於台灣正好處在 120-122 處, 也就是 51 zone 的邊緣, 因此 utm 對台灣來說還是有稍大的投影扭曲。
以下我使用 proj.4 進行地圖投影, 以 wgs84 作參考橢球經緯度, 將台灣各地的經緯度座標, 投影到 utm 51 及 twd97。 在圖面上以卡氏座標系計算距離, 再與大地線距離作比較大。
proj.4 ^4
proj.4 是 unix 系統下的投影轉換工具, 也是 QGIS 內部使用的投影轉換工具。 我使用 proj.4 最簡單的 command line 介面, 進行轉換測試。
使用 qgis 點出各地經緯度座標
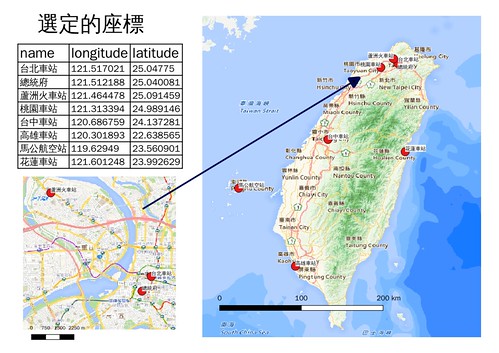
首先要選定一些點座標來作轉換, 為了能讓資料與現實生活連結, 而不只是單純無感情的數據, 選定了台灣各地及澎湖縣的交通樞鈕。
其中使用了 tgos 的 wms 圖層介接作為底圖 與數化座標的參考,因此座標可能不是很準確。 數化後再將座標存到該圖層屬性資料表中, 並將整體結果輸出為地圖,展示如下:
(查證後發現新北市蘆洲區並無火車站, 該點 蘆洲火車站 應更正為 捷運蘆洲站 。)
使用 invgeod 由經緯度計算大地線
invgeod 是 proj.4 所提供的工具, 可以由二點經緯度座標計算出大地線在二點上的方位角與長度。 這裡將上述各點分為七組,分別計算其 wgs84 橢球上的大地線長度:
$ invgeod +ellps=WGS84 <<GEOD
25.04775dN 121.517021dE 25.040081dN 121.512188dE
25.04775dN 121.517021dE 25.091459dN 121.464478dE
25.04775dN 121.517021dE 24.989146dN 121.313394dE
25.04775dN 121.517021dE 24.137281dN 120.686759dE
25.04775dN 121.517021dE 22.638565dN 120.301893dE
24.137281dN 120.686759dE 23.560901dN 119.62949dE
24.137281dN 120.686759dE 23.992629dN 121.601248dE
GEOD
-150d8'18.47" 29d51'34.164" 979.570
-47d34'55.949" 132d23'43.903" 7179.569
-107d29'8.833" 72d25'41.15" 21553.940
-140d0'17.414" 39d38'58.643" 131306.647
-154d51'50.457" 24d38'40.787" 294142.382
-120d26'28.284" 59d7'52.715" 125200.617
99d35'15.264" -80d2'22.26" 94373.816
| 路線 | 大地線長度 (m) |
|---|---|
| 台北車站-總統府 | 979.570 |
| 台北車站-蘆洲火車站 | 7179.569 |
| 台北車站-桃園車站 | 21553.940 |
| 台北車站-台中車站 | 131306.647 |
| 台北車站-高雄車站 | 294142.382 |
| 台中車站-馬公航空站 | 125200.617 |
| 台中車站-花蓮車站 | 117182.591 |
使用 proj 將經緯度投影到 twd97 平面座標
proj.4 的另一個工具 proj 可以將橢球座標投影到平面,
proj.4 本身帶有 epsg 的參數資料庫,
登記在 epsg 中的座標系統有現成的參數可以直接使用。
$ proj +init=epsg:3826 <<PROJ
121.5170212729008 25.047750402347074
121.51218835995553 25.040081355845224
121.46447770199445 25.091458666223513
121.3133939517849 24.98914581081843
120.68675863600342 24.1372808482334
120.30189266178539 22.638565387382755
119.62949045558962 23.560900758837473
121.60124825481569 23.99262920154155
PROJ
302168.39 2771166.16
301683.95 2770314.84
296849.94 2775988.28
281636.86 2764611.89
218164.11 2670262.31
178245.05 2504429.59
110084.00 2607064.50
311176.20 2654337.35
結果整理成表格:
| 地點 | 經度 | 緯度 | twd97 E | twd97 N |
|---|---|---|---|---|
| 台北車站 | 121.5170212729008 | 25.047750402347074 | 302168.39 | 2771166.16 |
| 總統府 | 121.51218835995553 | 25.040081355845224 | 301683.95 | 2770314.84 |
| 蘆洲火車站 | 121.46447770199445 | 25.091458666223513 | 296849.94 | 2775988.28 |
| 桃園車站 | 121.3133939517849 | 24.98914581081843 | 281636.86 | 2764611.89 |
| 台中車站 | 120.68675863600342 | 24.1372808482334 | 218164.11 | 2670262.31 |
| 高雄車站 | 120.30189266178539 | 22.638565387382755 | 178245.05 | 2504429.59 |
| 馬公航空站 | 119.62949045558962 | 23.560900758837473 | 110084.00 | 2607064.50 |
| 花蓮車站 | 121.60124825481569 | 23.99262920154155 | 311176.20 | 2654337.35 |
再依之前的分組方式,簡單用畢氏定理計算各分組二點間座標, 使用 octave 的 norm 函數,最後結果如下表:
| 路線 | twd97 平面投影距離 |
|---|---|
| 台北車站-總統府 | 979.503882585725 |
| 台北車站-蘆洲火車站 | 7179.04949815062 |
| 台北車站-桃園車站 | 21552.3126224032 |
| 台北車站-台中車站 | 131294.729532990 |
| 台北車站-高雄車站 | 294117.989881817 |
| 台中車站-馬公航空站 | 125200.931971005 |
| 台中車站-花蓮車站 | 94365.5299204625 |
使用 proj 將經緯度投影到 utm 51 zone 平面座標
utm 51 zone 的地圖投影作法也類似,
只是可以不用 epsg 代碼,
proj 有內建 utm 的投影參數:
proj +proj=utm +zone=51 。
結果如下二表:
| 地點 | utm 51 zone E | utm 51 zone N |
|---|---|---|
| 台北車站 | 350400.14 | 2771054.89 |
| 總統府 | 349903.20 | 2770210.87 |
| 蘆洲火車站 | 345153.83 | 2775954.94 |
| 桃園車站 | 329774.20 | 2764804.50 |
| 台中車站 | 264925.20 | 2671366.80 |
| 高雄車站 | 222690.52 | 2506024.50 |
| 馬公航空站 | 155892.74 | 2609662.42 |
| 花蓮車站 | 357713.83 | 2654116.80 |
| 路線 | utm 51 平面投影距離 (m) |
|---|---|
| 台北車站-總統府 | 979.448377404360 |
| 台北車站-蘆洲火車站 | 7178.73656144298 |
| 台北車站-桃園車站 | 21552.1872680176 |
| 台北車站-台中車站 | 131315.195829926 |
| 台北車站-高雄車站 | 294195.266216329 |
| 台中車站-馬公航空站 | 125281.713928394 |
| 台中車站-花蓮車站 | 94378.4528230724 |
成果分析
最後把三種投影的距離製表比較:
| 路線 | 大地線距離 | twd97 平面投影距離 | twd97 誤差 | utm 51 平面投影距離 (m) | utm 51 zone 誤差 |
|---|---|---|---|---|---|
| 台北車站 -總統府 | 979.57 | 979.503882585725 | 6.74963650122267E -05 | 979.44837740436 | 0.000124159167431 |
| 台北車站 -蘆洲火車站 | 7179.569 | 7179.04949815062 | 7.23583615368142E -05 | 7178.73656144298 | 0.000115945477649 |
| 台北車站 -桃園車站 | 21553.94 | 21552.3126224032 | 7.55025576205657E -05 | 21552.1872680176 | 8.13184031504352E -05 |
| 台北車站 -台中車站 | 131306.647 | 131294.72953299 | 9.07605767284862E -05 | 131315.195829926 | -6.5105842859602E -05 |
| 台北車站 -高雄車站 | 294142.382 | 294117.989881817 | 8.2926227825831E -05 | 294195.266216329 | -0.000179791215293 |
| 台中車站 -馬公航空站 | 125200.617 | 125200.931971005 | -2.51573045367377E -06 | 125281.713928394 | -0.000647735852564 |
| 台中車站 -花蓮車站 | 94373.816 | 94365.5299204625 | 8.78006197979934E -05 | 94378.4528230724 | -4.91325165063711E -05 |
可以看到,相較於 utm 51 zone,twd97 平面投影上的距離, 在台灣西部的誤差較小,整體表現優於 utm。 只有在台中到花蓮、台北到台串二段路線,誤差稍大於 utm。 整體來說,twd97 的誤差都在 0.0001 以下, 符合預期的 0.9999 精度。