legendre 球諧函數的正交性與系數
物理大地測量的各項球諧函數滿足正交性, 因此可以用多階球諧函數的和擬合地球重力位, 將各階球諧函數視作是總合函數的基底。 由於其正交性質,使用內積,(對函數也就是積分。) 就能由總合中分離出各項系數。 本次作業練習由 legendre 函數定義出各階球諧函數, 再以任意系數組合出一組重力位, 最後再嘗試從合成的重力位裡分離出各項系數。
legendre 函數
legendre 函數是一系列的遞迴函數, 總合稱為 legendre 級數。 用遞迴的定義方法, 可以由第一二階定義出任意階數, 而第 n 階的第 m 次,則需要以微分計算, 這裡使用數值微分。
global p0
global p1
p0 = @(t) ones(1,columns(t));
p1 = @(t) t;
function pn = p_nth(n)
global p0
global p1
if (n == 0)
pn = p0;
elseif (n == 1)
pn = p1;
else
pn_m1 = p_nth(n-1);
pn_m2 = p_nth(n-2);
pn = @(t) -(n-1)/n .* pn_m2(t) + (2*n-1) / n .* t .* pn_m1(t);
end
end
function dydx = derive_at (f, x, dx = 0.005)
dydx = ( f(x.+dx) .- f(x.-dx) ) / (dx*2);
end
function dfdx = derive (f, dx = 0.005)
dfdx = @(x) derive_at(f, x, dx);
end
function pnm = p_nmth(n,m)
dpnm = p_nth(n);
i = 0;
while (i < m)
dpnm = derive(dpnm);
i++;
end
pnm = @(t) (1-t.^2).^(m/2) .* dpnm(t);
end
呼叫 p_nth 可以取得第 n 階的 legendre 函數,
呼叫 p_nmth 則可以取得第 n 階第 m 次的 legendre 函數,
其返回值都是函數,而且各次呼叫間獨立;
如果要計算高階項效率會很差,
但本次作業最高階只用到 6,所以還能接受。
球諧函數
球諧函數就是將 legendre 函數
輸入定義在 cos(ψ) ,再乘上正弦或餘弦函數。
這裡也用高階函數的型式,重新包裝前面定義的 p_nmth ,
使其接受 ψ 作為輸入,再分別定義 rnm snm
為原函數乘上正弦或餘弦的結果。
p_nmth_cos = @(n,m) @(r) p_nmth(n,m)(cos(r));
global rnm
rnm = @(n,m) @(th,l) p_nmth_cos(n,m)(th) * cos(m*l);
global snm
snm = @(n,m) @(th,l) p_nmth_cos(n,m)(th) * sin(m*l);
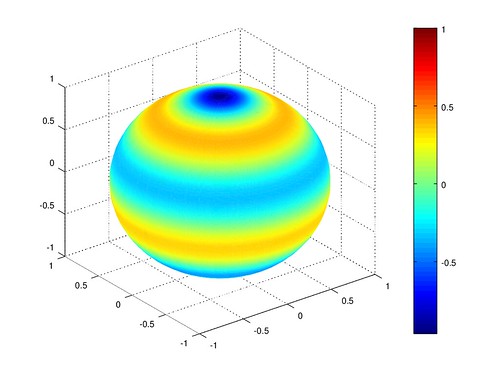
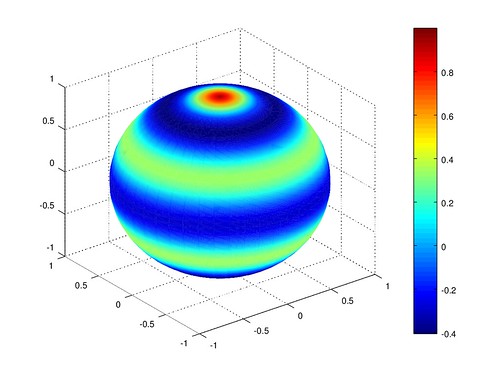
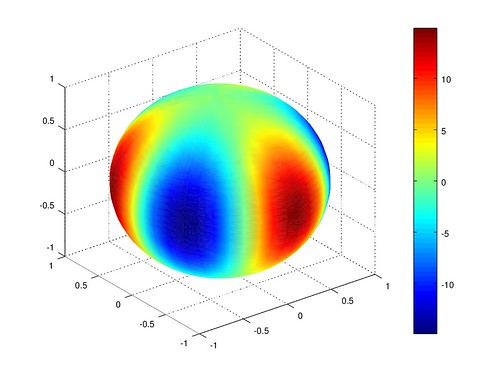
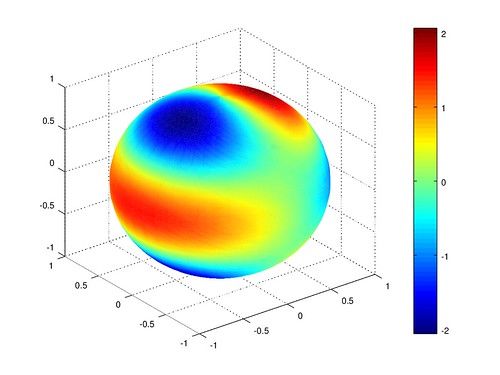
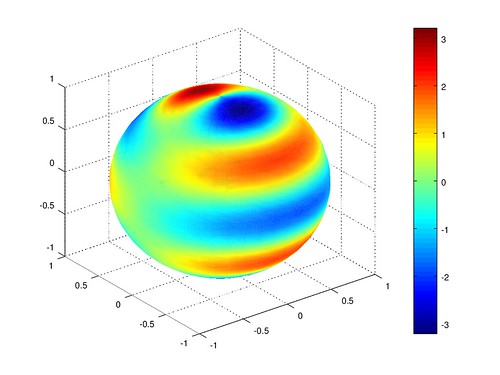
各階各次球諧函數圖型
在繪圖時,發現如果用 180 * 360 的球去畫, 我的程式會 buffer overflow, 所以就簡化成 45 * 45 的球, 每 8° 經度 4° 緯度取樣一次。 網格會變比較粗糙,但色階大致正確。
q1_rnm = [2 0
3 1
4 0
4 4
5 0
6 0];
q1_snm = [2 1
3 3
4 2
4 2
5 1
6 1];
global x_degree_range = 0:359;
global x_radian_range = x_degree_range /180 *pi;
global y_degree_range = 0:179;
global y_radian_range = y_degree_range /180 *pi;
function hdl = plot_earth_grid_180x360(grid)
% grid (latitude, longitude) = (1:180, 1:360)
grid_square = grid(1:4:end,1:8:end);
[x y z] = sphere(44);
hdl = surf(x,y,z, 'cdata', grid_square);
colorbar;
shading interp;
end
function plot_grid_180x360_tofile(grid, name)
fig = figure('visible', 'off');
plot_earth_grid_180x360(grid);
print('-dpng', [name '-sphere.png']);
close(fig);
end
for i=1:rows(q1_rnm)
n = q1_rnm(i,1);
m = q1_rnm(i,2);
frnm = rnm(n, m);
gridi = frnm(y_radian_range', x_radian_range);
plot_grid_180x360_tofile(gridi, ['r' num2str(n) num2str(m)]);
n = q1_snm(i,1);
m = q1_snm(i,2);
fsnm = snm(n, m);
gridi = fsnm(y_radian_range', x_radian_range);
plot_grid_180x360_tofile(gridi, ['s' num2str(n) num2str(m)]);
end
帶諧
扇諧
田諧
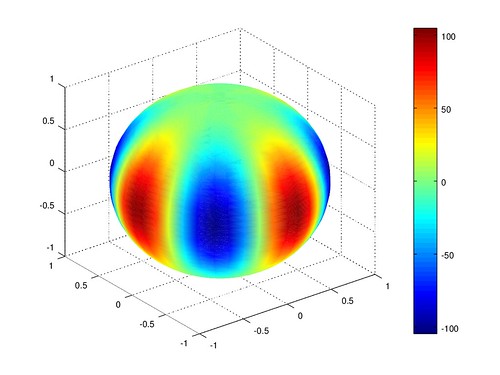
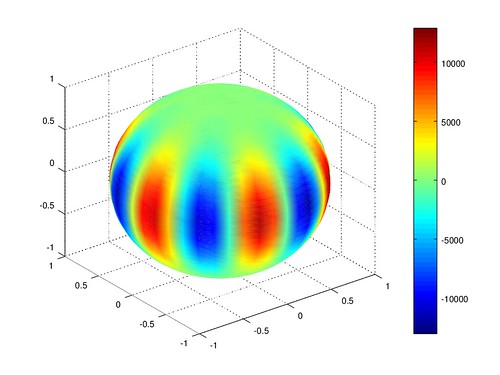
合成球諧函數
先隨機產生 n=0:6 m=0:n 的系數,
再將這些系數乘上各球諧函數,
加總得到合成的球諧函數網格。
系數是隨機產生的,在 0 1 之間。
global coefficient_data
coefficient_data = {};
function xnm = coefficient_xnm(type, n, m, set_value = [])
global coefficient_data
if (type == 'r')
type_id = 1;
else
type_id = 2;
end
if (isempty(set_value))
xnm = coefficient_data{type_id, n+1, m+1};
else
xnm = coefficient_data{type_id, n+1, m+1} = set_value;
end
end
coefficient_sum_grid = zeros(columns(y_radian_range), columns(x_radian_range));
for n = 0:6
for m = 0:n
% cell start from 1
rnmc = rand(1);
coefficient_xnm('r', n, m, rnmc);
coefficient_sum_grid += rnmc * rnm(n, m)(y_radian_range', x_radian_range);
snmc = rand(1);
coefficient_xnm('s', n, m, snmc);
coefficient_sum_grid += snmc * snm(n, m)(y_radian_range', x_radian_range);
end
end
plot_grid_180x360_tofile(coefficient_sum_grid, 'coefficient-sum');
| 系數名 | 系數值 | 系數名 | 系數值 |
|---|---|---|---|
| R00 | 0.909636 | S00 | 0.121664 |
| R10 | 0.109366 | S10 | 0.8308 |
| R11 | 0.824859 | S11 | 0.214129 |
| R20 | 0.832324 | S20 | 0.503761 |
| R21 | 0.117922 | S21 | 0.126986 |
| R22 | 0.695958 | S22 | 0.684922 |
| R30 | 0.868858 | S30 | 0.517931 |
| R31 | 0.638108 | S31 | 0.0319404 |
| R32 | 0.532819 | S32 | 0.572462 |
| R33 | 0.145508 | S33 | 0.0404046 |
| R40 | 0.916369 | S40 | 0.394033 |
| R41 | 0.199658 | S41 | 0.970572 |
| R42 | 0.784488 | S42 | 0.242452 |
| R43 | 0.707329 | S43 | 0.621902 |
| R44 | 0.766017 | S44 | 0.200479 |
| R50 | 0.761956 | S50 | 0.158401 |
| R51 | 0.814694 | S51 | 0.413291 |
| R52 | 0.759872 | S52 | 0.589732 |
| R53 | 0.448917 | S53 | 0.839896 |
| R54 | 0.357891 | S54 | 0.949848 |
| R55 | 0.89479 | S55 | 0.289316 |
| R60 | 0.520243 | S60 | 0.98437 |
| R61 | 0.916618 | S61 | 0.384952 |
| R62 | 0.107338 | S62 | 0.852719 |
| R63 | 0.561965 | S63 | 0.202933 |
| R64 | 0.571826 | S64 | 0.246472 |
| R65 | 0.0793381 | S65 | 0.0376952 |
| R66 | 0.707811 | S66 | 0.957893 |
估計各項球諧系數的振幅
由之後分離系數所使用的積分,其積分結果產生的系數
2*pi/(2*n+1)*factorial(n+m)/factorial(n-m) 可以得知,
雖然各項球諧的系數都介於 0-1 之間,
但 m 的次數越高,其結果的振幅也會越大,
產生的系數也會越大,二者約是階乘的關係。
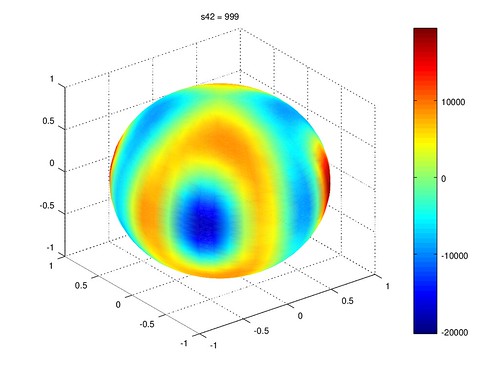
我選取了 S42 項作實驗,其圖形如上述圖九。 在維持其它系數不變,獨立調整 S42 係數, 繪出 B42 為 500 與 999 的情況如下。 在 500 時就能在原本合成的彩度中看出 S42 的形狀, 到 999 時則是二者混合,再增加就和 S42 的獨立圖形無太大區別了, 也就不畫了。
以正交性質分離系數
因為球諧函數各項間為正交, 故在函數上積分後如同內積, 可以消去其它所有正交的不同次項, 只留下原本的項。 可以運用此一性質從合成的函數結果中, 分離出各項的系數。
function coefficient = coefficient_devide(grid_all, sh_type, n, m)
global x_radian_range
global y_radian_range
global rnm
global snm
if (sh_type == 'r')
fnm = rnm(n,m);
else % 's'
fnm = snm(n,m);
end
if (m == 0)
coefficient_integral = 4*pi/(2*n+1);
else
coefficient_integral = 2*pi/(2*n+1)*factorial(n+m)/factorial(n-m);
end
grid_single = fnm(y_radian_range', x_radian_range);
grid_sin = sin(y_radian_range' * ones(size(x_radian_range)));
sum2d = @(grid) sum(sum(grid));
grid_integral = sum2d(grid_single .* grid_all .* grid_sin) * (
pi*2*pi /180/360
);
coefficient = grid_integral / coefficient_integral;
end
for n=0:6
for m = 0:n
printf('R%d%d %d\n',
n, m, coefficient_devide(coefficient_sum_grid, 'r', n,m));
printf('S%d%d %d\n',
n, m, coefficient_devide(coefficient_sum_grid, 's', n,m));
end
end
其中 Snm 中 m=0 的項是 0,
所以該項的系數其實是沒有意義的;
但我在產生系數時沒有特別濾掉,
所以這裡也才會有數值,但分離出來還是 0。
分離出的系數都相當準確,可以準確到小數下第二位。
| 系數名 | 系數真值 | 分離出的系數值 | 系數名 | 系數值 | 分離出的系數值 |
|---|---|---|---|---|---|
| R00 | 0.909636 | 0.909555 | S00 | 0.121664 | 0 |
| R10 | 0.109366 | 0.109233 | S10 | 0.8308 | 0 |
| R11 | 0.824859 | 0.825042 | S11 | 0.214129 | 0.214204 |
| R20 | 0.832324 | 0.83192 | S20 | 0.503761 | 0 |
| R21 | 0.117922 | 0.118295 | S21 | 0.126986 | 0.127272 |
| R22 | 0.695958 | 0.696267 | S22 | 0.684922 | 0.685633 |
| R30 | 0.868858 | 0.868548 | S30 | 0.517931 | 0 |
| R31 | 0.638108 | 0.638342 | S31 | 0.0319404 | 0.032054 |
| R32 | 0.532819 | 0.533218 | S32 | 0.572462 | 0.572772 |
| R33 | 0.145508 | 0.145862 | S33 | 0.0404046 | 0.041066 |
| R40 | 0.916369 | 0.915642 | S40 | 0.394033 | 0 |
| R41 | 0.199658 | 0.200045 | S41 | 0.970572 | 0.970741 |
| R42 | 0.784488 | 0.784601 | S42 | 0.242452 | 0.243179 |
| R43 | 0.707329 | 0.708025 | S43 | 0.621902 | 0.622153 |
| R44 | 0.766017 | 0.766961 | S44 | 0.200479 | 0.200886 |
| R50 | 0.761956 | 0.761469 | S50 | 0.158401 | 0 |
| R51 | 0.814694 | 0.814834 | S51 | 0.413291 | 0.413305 |
| R52 | 0.759872 | 0.759934 | S52 | 0.589732 | 0.589799 |
| R53 | 0.448917 | 0.448923 | S53 | 0.839896 | 0.839898 |
| R54 | 0.357891 | 0.357891 | S54 | 0.949848 | 0.949848 |
| R55 | 0.89479 | 0.89479 | S55 | 0.289316 | 0.289316 |
| R60 | 0.520243 | 0.519194 | S60 | 0.98437 | 0 |
| R61 | 0.916618 | 0.916692 | S61 | 0.384952 | 0.385246 |
| R62 | 0.107338 | 0.107558 | S62 | 0.852719 | 0.852801 |
| R63 | 0.561965 | 0.56207 | S63 | 0.202933 | 0.203026 |
| R64 | 0.571826 | 0.571866 | S64 | 0.246472 | 0.246483 |
| R65 | 0.0793381 | 0.0793381 | S65 | 0.0376952 | 0.037695 |
| R66 | 0.707811 | 0.707811 | S66 | 0.957893 | 0.957893 |