傅立葉三角函數基底練習
物理大地測量的作業一,用三角函數當基底, 嘗試合成出新的函數,再用正交基底的概念, 將合成函數分解回基底,等同於計算傅立葉轉換參數的過程; 並嘗試在合成函數中加入雜訊,測試含雜訊的分解。 最後再嘗試用測量界通用的最小二乘平差法求解參數, 分析不同做法的差異。
程式
本作業使用相容於 matlab 的程式語言 octave。
基底函數
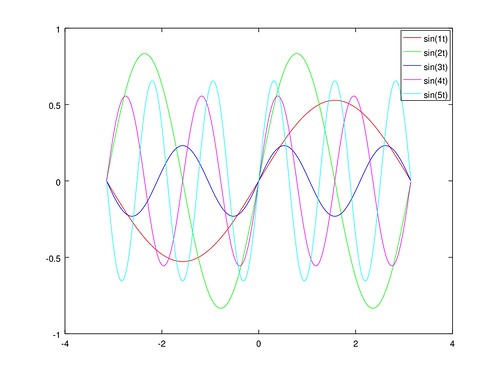
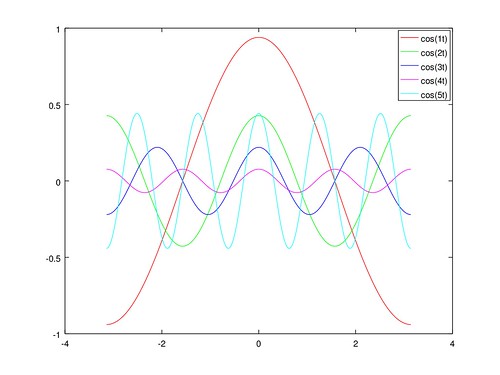
試以 sin(t), cos(t), sin(2t), cos(2t), sin(3t), cos(3t), sin(4t), cos(4t), sin(5t), cos(5t) 為基底, 在每項給定任意系數,合成出新的函數。
首先產生十個函數基底,存入 2 x 5 的結構體:
global basis = {};
for i = 1:5
basis{1,i} = @(t) sin(i * t);
basis{2,i} = @(t) cos(i * t);
end
產生同樣 2 x 5 矩陣的任意系數:
global coeffiecient = rand(2,5);
disp(coeffiecient);
| t | 1 | 2 | 3 | 4 | 5 |
|---|---|---|---|---|---|
| cos | 0.9396886768956427 | 0.4270019532953698 | 0.220015914369331 | 0.07659683799706178 | 0.4415894405693337 |
| sin | 0.527726636334051 | 0.8334814789927278 | 0.2312067814650228 | 0.5559265528546949 | 0.655401249470971 |
之後畫出各基底的圖形:
合成函數
合成函數 f 如果寫成 matlab 函數:
f(t) = 0.94 cos(t) + 0.43 cos(2t) + 0.22 cos(3t) +
0.08 cos(4t) + 0.44 cos(5t) + \\
0.53 sin(t) + 0.83 sin(2t) + 0.23 sin(3t) + 0.56 sin(4t) + 0.66 sin(5t)
function sum = sum_function(t)
global coefficient basis;
sum = 0;
for i = [1:5]
sum += coefficient(1,i) * basis{1,i}(t);
sum += coefficient(2,i) * basis{2,i}(t);
end
end
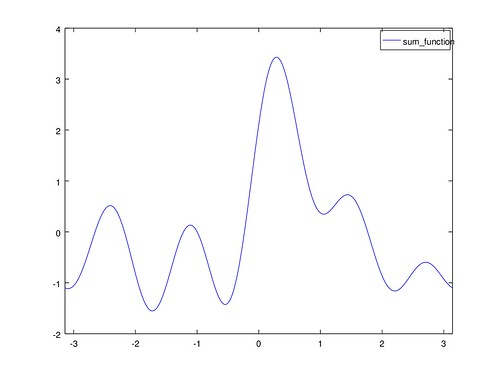
之後畫圖 fplot(@sum_function, [-pi, pi]) ,
結果如下:
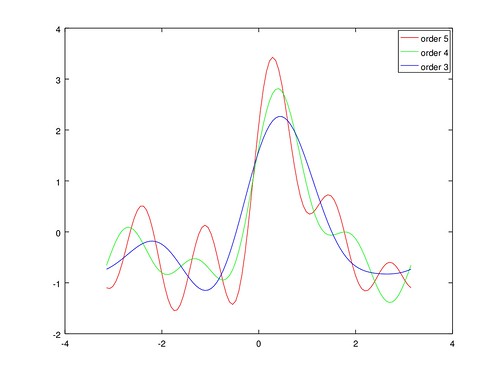
比較低階項的情況, 以下分別畫出只取到第三、四、五階的圖形:
雜訊
再來,嘗試為函數加入雜訊。 這裡先把之前合成函數的結果存起來, 再和隨機生成的雜訊相加。 這裡定義雜訊為 ±0.25。
range_t = linspace(-pi, pi, 100);
data = sum_function(range_t);
noise = (rand(1,100) .- 0.5) / 2;
noise_data = data + noise;
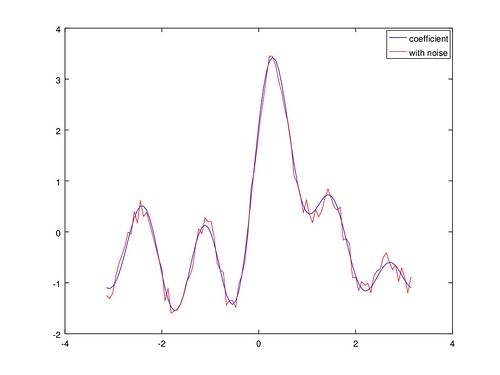
然後把這二個函數作圖比較, 由於是取樣後再作圖,看起來會稍微不連續。
plot(range_t, data, "b;coefficient;", range_t, noise_data, "r;with noise;");
因為之後還要對雜訊函數後的函數做積分或平差, 所以需要將雜訊的成果。 但 rand 函數是隨機的,每次運行都產生不同的結果, 只能運行後,把該次運行結果存下來, 之後就對該結果做積分或平差。 我是用簡單的取樣,在 [-π, π] 的區間中取樣一百次, 然後就用這一百次結果作圖。
積分
最後要試著對合成函數與加入雜訊後的函數做積分, 嘗試還原原始的參數。 但因為雜訊是不連續的,只能用不連續的小區間累加模擬積分。
function coefficient = restore_coefficient(data)
count = 100;
range_x = linspace(-pi, pi, count);
coefficient = zeros(2,5);
for i = 1:5
range = sum(data .* cos(i * range_x)) / count * 2 * pi;
coefficient(1,i) = range / pi;
range = sum(data .* sin(i * range_x)) / count * 2 * pi;
coefficient(2,i) = range / pi;
end
end
fcoefficient = restore_coefficient(data);
noise_fcoefficient = restore_coefficient(noise_data);
最後還原的參數如下:
| t | cos | sin | 直接還原 cos | 直接還原 sin | 雜訊 cos | 雜訊 sin |
|---|---|---|---|---|---|---|
| 1 | 0.939689 | 0.527727 | 0.952246 | 0.522449 | 0.922092 | 0.511869 |
| 2 | 0.427002 | 0.833481 | 0.400778 | 0.825147 | 0.401755 | 0.781798 |
| 3 | 0.220016 | 0.231207 | 0.239770 | 0.228895 | 0.224191 | 0.225057 |
| 4 | 0.076597 | 0.555927 | 0.053877 | 0.550367 | 0.027566 | 0.561177 |
| 5 | 0.441589 | 0.655401 | 0.459127 | 0.648847 | 0.464609 | 0.626823 |
結果有無雜訊的積分結果誤差竟然差不多, 應該是離散積分的效果太差了,可能 -π 到 π 只取樣 100 次太少吧; 不過還是有一些比較小的參數在加上雜訊後就完全跑掉了, 例如 t=4 時的 cos 函數。
精密數值積分
如果是用 matlab 內建的 quad 函數做比較精細的數值積分, 還原出來的參數幾乎一模一樣。 因此可以推斷,幾乎是取樣次數太少的問題。
qcoefficient = zeros(2,5);
for i = 1:5
qcoefficient(1,i) = quad(@(t) f(t) * cos(i * t), -pi, pi) / pi;
qcoefficient(2,i) = quad(@(t) f(t) * sin(i * t), -pi, pi) / pi;
end
| t | cos | sin | quad cos | quad sin | 離散積分 cos | 離散積分 sin |
|---|---|---|---|---|---|---|
| 1 | 0.939689 | 0.527727 | 0.939689 | 0.527727 | 0.952246 | 0.522449 |
| 2 | 0.427002 | 0.833481 | 0.427002 | 0.833481 | 0.400778 | 0.825147 |
| 3 | 0.220016 | 0.231207 | 0.220016 | 0.231207 | 0.239770 | 0.228895 |
| 4 | 0.076597 | 0.555927 | 0.076597 | 0.555927 | 0.053877 | 0.550367 |
| 5 | 0.441589 | 0.655401 | 0.441589 | 0.655401 | 0.459127 | 0.648847 |
取樣 999 次的結果
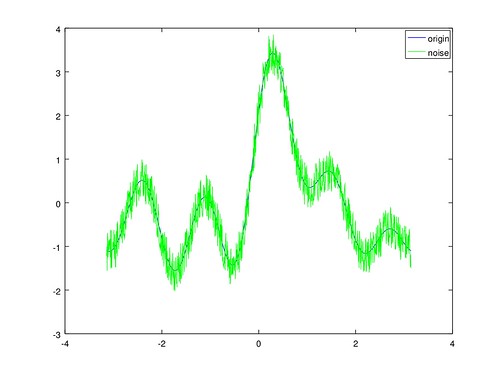
如果提升取樣次數,再次嘗試計算參數, 另外這裡提升誤差到 ±0.5。
range_x = linspace (-pi, pi, 999)
data = zeros(1,999)
data = call_value (cbasis ,range_x)
noise_data = data .+ rand(1,999) - 0.5;
plot(range_x, data, range_x, noise_data)
| t | cos | sin | 直接還原 cos | 直接還原 sin | 雜訊 cos | 雜訊 sin |
|---|---|---|---|---|---|---|
| 1 | 0.939689 | 0.527727 | 0.940946 | 0.527198 | 0.912194 | 0.534710 |
| 2 | 0.427002 | 0.833481 | 0.424377 | 0.832647 | 0.427413 | 0.816731 |
| 3 | 0.220016 | 0.231207 | 0.221993 | 0.230975 | 0.209362 | 0.214364 |
| 4 | 0.076597 | 0.555927 | 0.074323 | 0.555370 | 0.084341 | 0.571403 |
| 5 | 0.441589 | 0.655401 | 0.443345 | 0.654745 | 0.441065 | 0.664710 |
由於提升了取樣數,使積分結果更精確, 也就能看出加上雜訊確實會減弱用傅立葉轉換回推參數的精度。
最小二乘平差法還原參數
若使用最小二乘平差法還原參數, 用 999 次取樣當作 999 次觀測方程式, 而 cos sin 的參數則當作待求解參數:
L = A X + V
\\
\begin{bmatrix}
f(\pi) \\
f(\pi-0.001) \\
\vdots \\
f(-\pi)
\end{bmatrix}
=
\begin{bmatrix}
cos(\pi) & cos(2 \pi) & \cdots &
sin(\pi) & \cdots & sin(5 \pi) \\
cos(\pi - 0.001) & \ddots \\
\vdots \\
cos(-\pi) & \cdots
\end{bmatrix}
\begin{bmatrix}
a_1 \\
a_2 \\
\vdots \\
b_1 \\
\vdots \\
b_5
\end{bmatrix}
design_matrics = zeros(999, 10);
for i = 1:5
design_matrics(:,i) = cos(i * range_x');
design_matrics(:,i+5) = sin(i * range_x');
end
求解方法則是求出法方程矩陣的逆, 從而可以得到未知參數與誤差:
N = A^T A \\
\hat X = N^{-1} A^T L \\
V = L - A \hat X
normal_matrics = design_matrics' * design_matrics;
adjustment_coefficient = inv(normal_matrics) * design_matrics' * data';
adjustment_error = data' - design_matrics * adjustment_coefficient;
而帶雜訊的解算亦如下, 最後的結果如下表:
| t | cos | sin | 直接平差 cos | 直接平差 sin | 帶雜訊 cos | 帶雜訊 sin |
|---|---|---|---|---|---|---|
| 1 | 0.939689 | 0.527727 | 0.939689 | 0.527727 | 0.911021 | 0.535245 |
| 2 | 0.427002 | 0.833481 | 0.427002 | 0.833481 | 0.429929 | 0.817549 |
| 3 | 0.220016 | 0.231207 | 0.220016 | 0.231207 | 0.207485 | 0.214579 |
| 4 | 0.076597 | 0.555927 | 0.076597 | 0.555927 | 0.086512 | 0.571976 |
| 5 | 0.441589 | 0.655401 | 0.441589 | 0.655401 | 0.439420 | 0.665376 |
綜合結論
先上表,將有無雜訊的單獨製表:
無雜訊的
| t | cos | sin | 傅立葉轉換離散積分 cos | 傅立葉轉換離散積分 sin | 傅立葉轉換 quad 積分 cos | 傅立葉轉換 quad 積分 sin | 直接平差 cos | 直接平差 sin |
|---|---|---|---|---|---|---|---|---|
| 1 | 0.939689 | 0.527727 | 0.940946 | 0.527198 | 0.939689 | 0.527727 | 0.939689 | 0.527727 |
| 2 | 0.427002 | 0.833481 | 0.424377 | 0.832647 | 0.427002 | 0.833481 | 0.427002 | 0.833481 |
| 3 | 0.220016 | 0.231207 | 0.221993 | 0.230975 | 0.220016 | 0.231207 | 0.220016 | 0.231207 |
| 4 | 0.076597 | 0.555927 | 0.074323 | 0.555370 | 0.076597 | 0.555927 | 0.076597 | 0.555927 |
| 5 | 0.441589 | 0.655401 | 0.443345 | 0.654745 | 0.441589 | 0.655401 | 0.441589 | 0.655401 |
發現在平差的觀測方程式與積分的取樣數都是 999 的情況下, 平差的結果會優於傅立葉轉換的結果。 但內建的數值積分 quad 和平差的結果是差不多的, 因此這裡可以推論傅立葉轉換在這次作業上, 是和平差的精度相當的,只是受限於積分方法只用單純的取樣, 所以積分結果不夠精準。 如果用好的數值積分方法,例如使用 matlab 內的 quadpack, 就能達到和平差相當的精度。
帶雜訊的
| t | cos | sin | 傅立葉轉換 cos | 傅立葉轉換 sin | 直接平差 cos | 直接平差 sin |
|---|---|---|---|---|---|---|
| 1 | 0.939689 | 0.527727 | 0.912194 | 0.534710 | 0.911021 | 0.535245 |
| 2 | 0.427002 | 0.833481 | 0.427413 | 0.816731 | 0.429929 | 0.817549 |
| 3 | 0.220016 | 0.231207 | 0.209362 | 0.214364 | 0.207485 | 0.214579 |
| 4 | 0.076597 | 0.555927 | 0.084341 | 0.571403 | 0.086512 | 0.571976 |
| 5 | 0.441589 | 0.655401 | 0.441065 | 0.664710 | 0.439420 | 0.665376 |
帶雜訊的分析上,因為是用離散的隨機產生的雜訊, 因此也沒有所謂 絕對準確的積分 。 用積分與平差得到的結果不相上下, 二者的結果都比我預期的好,推論可能原因各是
因為雜訊是 999 份離散的雜訊,這次選取的傅立葉函數只到 5 階, 也就是 π/5 的解析度,根本看不到 2π/999 解析度的訊號, 因此也能夠免除掉其干擾。
平差上雖然看似使用到正弦餘弦等非線性函數,但那些只是基底, 真正的觀測方程式和係數的關係還是線性的, 因此平差也能夠簡單計算,達到精確的結果。
參考資料
物理大地測量,交通大學鄭景中教授授課,傅立葉轉換。Advanced Engineering Mathematics, 10/e (IE-Paperback), Erwin Kreyszig, ISBN:9780470646137, Fourier transform.
測量平差法,唐城,間接觀測平差。
octave help page quad
octave help page global
MathJax: https://mathjax.org/