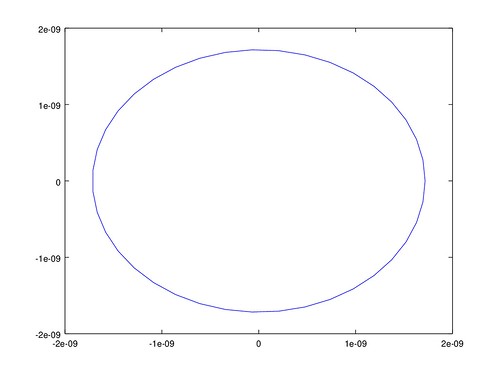
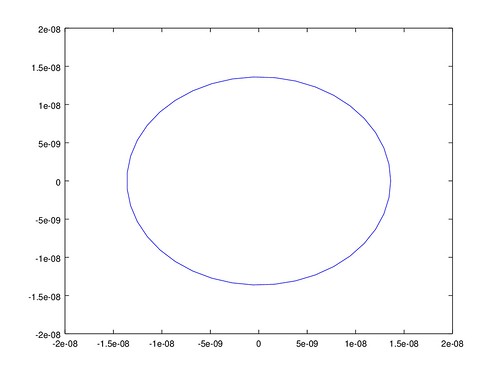
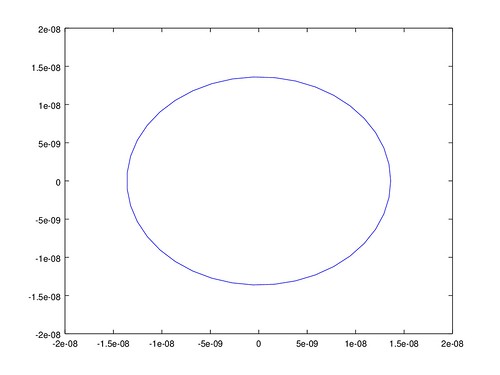
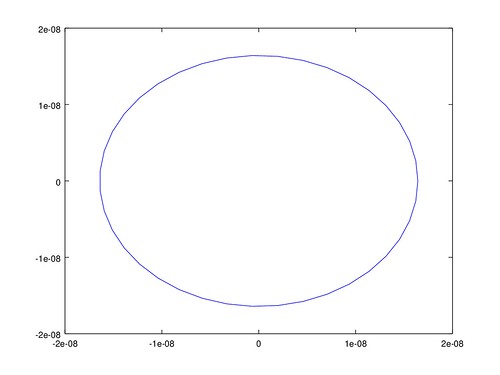
平差作業九

平差 GNSS 基線後的誤差橢圓計算。

變方協變方矩陣

平差過程與第八次作業大致相同，就不再列式， 直接進入間接觀測平差後，可以計算得所有未知數的變方協變方矩陣。

\hat \Sigma _ {\hat x} = \hat {\sigma_0} N^{-1} = \
\begin{bmatrix}
\sigma_{X_A} ^2  & \sigma_{X_A Y_A} & \dots \\
\sigma_{X_A Y_A} & \sigma_{Y_A} ^2  & \dots \\
\vdots
\end{bmatrix}

協變方矩陣中，各元素是變方或二未知數的協變方。 單一點上的 x y 座標的變方協變方矩陣， 就是其中的一小區塊。

%% xy_matrix(3) 就是取出第三點的 X Y 相關矩陣
xy_matrix = @(i) point_covariance_matrix(i*3-2:i*3-1, i*3-2:i*3-1);

誤差橢圓

有了 x y 的協變方矩陣，就能計算平面上的誤差橢圓。 誤差橢圓可以用三個參數表示， 分別是橢圓的長軸長、短軸長、長軸角度。

C_1 = \hat {\sigma_0} \sqrt \lambda_1 \\
C_2 = \hat {\sigma_0} \sqrt \lambda_2 \\
\theta = \frac{1}{2} arctan (
\frac { 2 \sigma_{x y} } {\sigma_x^2 - \sigma_y^2} )

function elips_parameter = compute_error_elips(xy_covariance, sigma0)
  eigenvalue = eig(xy_covariance);
  elips_parameter = zeros(1, 3);
  elips_parameter(1:2) = sqrt(eigenvalue(1:2)) * sigma0;

  orintation2 = atan2(
      2*xy_covariance(1,2),
      (xy_covariance(1,1) - xy_covariance(2,2))
  );
  elips_parameter(3) = orintation2 / 2;
end

繪圖

要從橢圓參數畫出誤差橢圓，我是用參數式與 sin cos 計算。

function xy = compute_ellipse_xy(long, short, orientation)
  m = 40;
  x = zeros(m,1);
  y = zeros(m,1);
  theta = linspace(0,2*pi,m);
  for k = 1:m
    x(k) = long * cos(theta(k));
    y(k) = short * sin(theta(k));
  end
  alpha = -orientation;
  R  = [cos(alpha) -sin(alpha)
        sin(alpha)  cos(alpha)];
  rCoords = R*[x' ; y'];
  xr = rCoords(1,:)';
  yr = rCoords(2,:)';

  xy = [xr'; yr'];
end

function plot_name(todo, file)
  fig = figure('visible', 'off');
  todo();
  print('-dpng', file);
  close(fig);
end


for i = 1:rows(point_vector)
  elips_parameter = compute_error_elips(
                        xy_matrix(i), variance_post);
  elips_xy = compute_ellipse_xy(
                 elips_parameter(1),
                 elips_parameter(2),
                 elips_parameter(3));
  plot_name(@() plot(elips_xy(1,:), elips_xy(2,:)),
            ['ellipse-' num2str(i) '.png']);
end

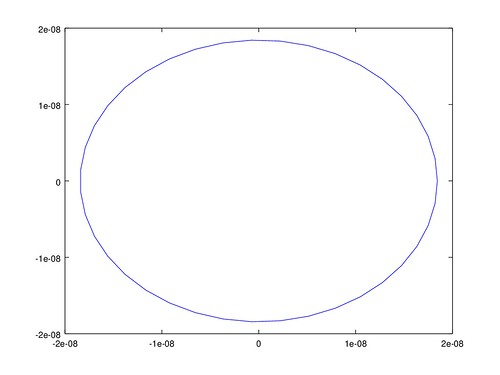
但繪圖結果中的 X Y 座標軸好像不一致， 所以看起來變成橢圓，其實都是正圓。 從協變方矩陣中各點的 $\sigma_{x y}$ 都為 0， 也就是各點的 x y 座標無相關， 誤差橢圓的長短軸等長，即為正圓。